INECUACIONES

INECUACIONES

  Una inecuación es una desigualdad algebraica en la que aparecen una o más incognitas en los miembros de la desigualdad. Si la desigualdad es del tipo o 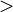se denomina inecuación en sentido estricto y si es del tipo o 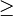se denomina inecuación en sentido amplio.
Del mismo modo en que se hace la diferencia entre igualdad y ecuacion, una inecuación que es válida para todos las variables se llama inecuación incondicional y las que son válidas solo para algunos valores de las variables se conocen como inecuaciones condicionales. Los valores que verifican la desigualdad, son sus soluciones.
 

• Ejemplo de inecuación incondicional: .
• Ejemplo de inecuación condicional:  

Los criterios más comunes de clasificación de las inecuaciones son:
 

• Según el número de incógnitas,
  • De una incógnita. Ejemplo: .
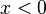  • De dos incógnitas. Ejemplo: .
  • De tres incógnitas. Ejemplo: .
  • etc.

Según la potencia de la incógnita,

• De primer grado o lineal. Cuando el mayor exponente de la incógnita de la inecuación es uno. Ejemplo: .

• De segundo grado o cuadrática. Cuando el mayor exponente de cualquiera de sus incógnitas es dos. Ejemplo: .

• De tercer grado o cúbica. Cuando el mayor exponente de cualquiera de sus incógnitas es tres. Ejemplo: .

IMAGEN DE LA INECUACION

 PASOS PARA REALIZAR LAS IN ECUACIONES

 1º Quitar paréntesis
  
2º Quitar denominadores. 

3º Agrupar los términos en x a un lado de la desigualdad y los términos           independientes en el otro.

4º Efectuar las operaciones

5º Como el coeficiente de la x es negativo multiplicamos por −1, por lo que cambiará el sentido de la desigualdad.

6º Despejamos la incógnita.



.

Máximos y Mínimos(función cuadrática)

Máximos y Mínimos

Se establece si una función cuadrática tiene un máximo o un mínimo. Se usa la fórmula del vértice para conseguir el mayor o menor valor de la función.                                                                                                          La discusión se basa en la gráfica de la función: la parábola. Se muestran dos ejemplos que explican como determinar el máximo o mínimo de la función dada y dónde ocurre o se alcanza ese máximo.


 La teoría de optimizacion clásica se usa para la obtención de los
máximos y mínimos de funciones no lineales restringidas y no restringidas, en los que 
se hace uso del calculo diferencial.

          

Mínimo (fuerte): Un punto extremo X0 de una función f(X0) define un mínimo de la 
función si f(X0+h) > f(X0), donde X0  es cualquier punto de la función y h en valor 
absoluto es suficientemente pequeña.
Máximo (fuerte): Un punto extremo X0 de una función f(X0) define un máximo de la 
función si f(X0+h) < f(X0), donde X0  es cualquier punto de la función y h en valor 
absoluto es suficientemente pequeña.

 

Funciones Cuadráticas

Cuales son las funciones cuadráticas?

Una función cuadrática es aquella que puede escribirse de la forma:

f(x)=axª+bx+c 

donde a, b y c son números reales cualesquiera y a distinto de cero.

Si representamos "todos" los puntos (x,f(x)) de una función cuadrática, obtenemos siempre una curva llamada parábola.

Como ejemplo, ahí tienes la representación gráfica de dos funciones cuadráticas muy sencillas:

f(x) = x²

f(x) = -x²

Intersección de la parábola con los ejes

• Intersección con el eje Y: Como todos los puntos de este eje tienen la abscisa x = 0, el punto de corte de la parábola con el eje Y tendrá de coordenadas (0,c)
• Intersección con el eje X: Como todos los puntos del eje X tienen la ordenada y = 0, para ver estos puntos de corte se resuelve la ecuación de segundo grado ax² + bx + c = 0.Dependiendo del valor  (D) de la ecuación, se pueden presentar tres situaciones distintas:
  
  Si D > 0, la ecuación tiene dos soluciones reales y distintas y la parábola cortará al eje X en dos puntos.
  
  Si D = 0, la ecuación tiene una solución real y, por tanto, la parábola cortará al eje X en un punto (que será el vértice).
  
  Si D < 0, la ecuación no tiene soluciones reales y la parábola no cortará al eje X.

PROCEDIMIENTO PARA REALIZAR UNA FUNCIÓN CUADRÁTICA

Concepto de Matematicas

Que son las matemáticas?

El término matemáticas viene del griego "máthema", que quiere decir aprendizaje, estudio y ciencia. Y justamente las matemáticas son una disciplina académica que estudia conceptos como la cantidad, el espacio, la estructura y el cambio. 

El alcance del concepto ha ido evolucionando con el tiempo, desde el contar y calcular hasta abarcar lo mencionado anteriormente. Aunque algunos las consideran como una ciencia abstracta, la verdad es que no se puede negar que esta inspirada en las ciencias naturales, y uno de sus aplicaciones más comunes se lleva a cabo en la Física.

La historia de las matemáticas comienza con la primera gran "abstracción", que es el desarrollo de los números y el contar. Los orígenes de esta disciplina vienen dados por una necesidad bastante básica: la necesidad de contar objetos físicos para el comercio (en sus inicios el trueque), para clasificar extensiones de territorio y para realizar asociaciones relacionadas con los astros. Por supuesto que la siguiente necesidad fue la de realizar operaciones básicas con estos números, para poder hacer predicciones básicas: el sumar, restar, multiplicar y dividir. Además, paralelamente se desarrollaron los conceptos geométricos, de los cuales tenemos pruebas sólidas como los antiguos monumentos monolíticos.

Símbolos Matemáticos

Importancia de las Matemáticas 

La importancia de las matemáticas existe porque día a día nos encontramos frente a ellas, sin ellas no podríamos hacer la mayoría de nuestra rutina, necesitamos las matemáticas constantemente, en la escuela, en la oficina. En las matemáticas han tenido mayor importancia porque representan la base de todo un conjunto de conocimientos que el hombre ha ido adquiriendo.